트리(Tree)란?
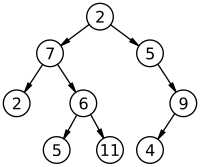
: 노드 N개와 N-1개의 간선으로 이루어져 있으며 모든 노드가 서로 연결되어 있는 구조
- 하나의 루트 노드를 갖는다.
- 사이클이 존재할 수 없다.
- 비선형 자료구조로 계층적이다.
신장 트리란(Spanning Tree)란?
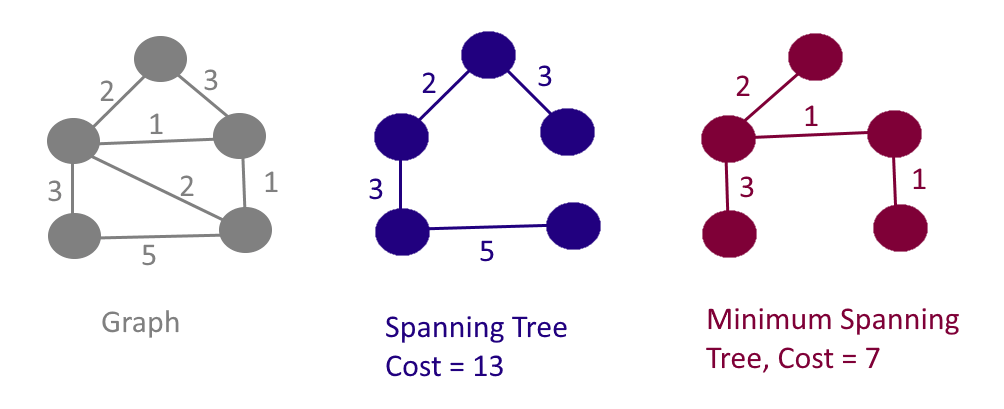
: 그래프 상에서 모든 노드가 사이클 없이 연결된 부분 그래프
- 양방향 그래프
최소 신장 트리(MST, Minum Spanning Tree)
: 양방향 가중 그래프에서 정의되며, 신장 트리 중에서 가중치의 합이 최소가 되는 신장 트리
접근 방법
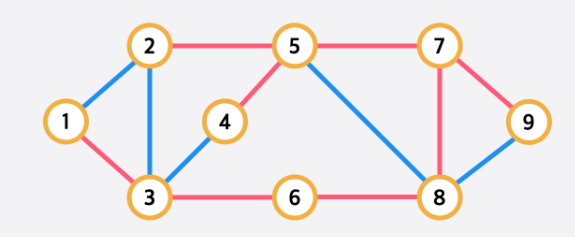
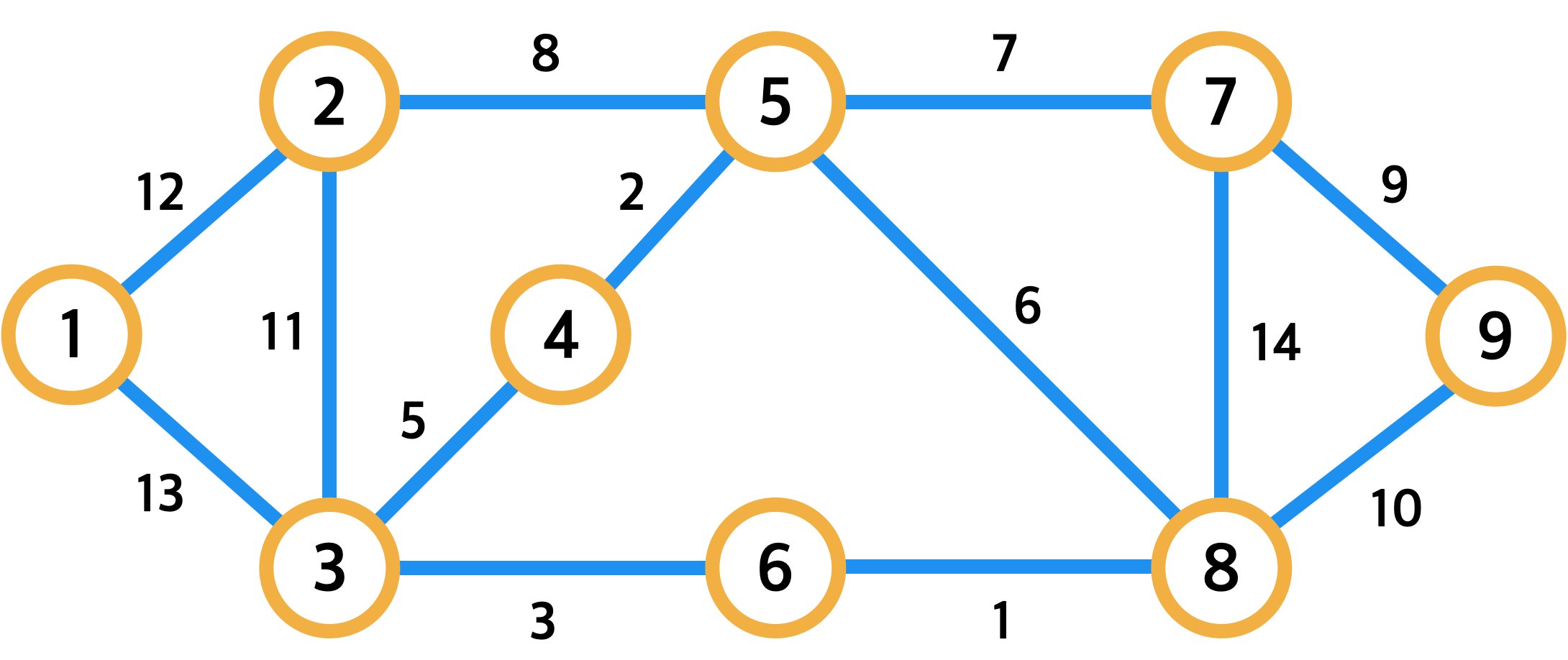
: N 개의 도시가 있을 때, 최소한의 비용만 투자하여 모든 도시를 이어주려면 ?
→ MST(Miniumum Spanning Tree) 알고리즘 사용 !
크루스칼 알고리즘
: 양방향 가중 그래프의 최소 신장 트리(MST)를 찾는 알고리즘
: 그리디 기반으로 가중치가 낮은 간선을 추가해 가면서 최소 신장 트리를 찾는 방식
- 사이클을 가지면 안된다는 조건에 유의할 것 !
function kruskal()
mst = [] // mst를 담을 배열입니다.
sort edge[] by length // 간선을 가중치 기준으로 오름차순 정렬합니다.
uf = uf_init(|V|) // uf 배열을 노드의 수 |V|만큼 초기화합니다.
for E in edge[] // 각각의 간선에 대해
u, v = E // 간선을 이루고 있는 두 노드 u, v를 보며
if find(u) != find(v) // u, v의 루트 노드가 다른 경우에만
mst.push(E) // mst에 해당 간선을 넣어주고
union(u, v) // u, v를 같은 루트 노드를 갖도록 만들어줍니다.
return mst
# 변수 선언 및 입력:
n, m = tuple(map(int, input().split()))
edges = [
tuple(map(int, input().split()))
for _ in range(m)
]
uf = [0] * (n + 1)
def find(x):
if uf[x] == x:
return x
uf[x] = find(uf[x])
return uf[x]
def union(x, y):
X, Y = find(x), find(y)
uf[X] = Y
# cost 순으로 오름차순 정렬을 진행합니다.
edges.sort(key=lambda x: x[2])
# uf 값을 초기값을 적어줍니다.
for i in range(1, n + 1):
uf[i] = i
# cost가 낮은 간선부터 순서대로 보며
# 아직 두 노드가 연결이 되어있지 않을 경우에만
# 해당 간선을 선택하고 두 노드를 합쳐주면서
# mst를 만들어줍니다.
ans = 0
for x, y, cost in edges:
# x, y가 연결되어 있지 않다면
if find(x) != find(y):
# 해당 간선은 MST에 속하는 간선이므로
# 답을 갱신해주고
# 두 노드를 연결해줍니다.
ans += cost
union(x, y)
print(ans)
REFERENCE
코드트리
'[Algorithm] 알고리즘' 카테고리의 다른 글
| [Algorithm] 재귀 함수와 리턴(return) (1) | 2024.07.18 |
|---|---|
| [백준][Python] 1926번 그림 - DFS,BFS (6) | 2024.07.16 |
| 이진 탐색 (0) | 2024.07.09 |
| 그래프 (1) | 2024.07.09 |
| 플로이드 워셜 알고리즘 (0) | 2024.07.09 |
