플로이드 워셜 알고리즘이란?
: 그래프에서 모든 노드 쌍에 대한 최단 거리를 구하는 알고리즘.
: 시간복잡도 - O(V^3)
- 인접 행렬을 사용
- 음의 가중치를 가지는 그래프에서도 쓸 수 있다.
- But, 음수 사이클은 존재해서는 안된다.
음수 사이클이란? 사이클의 모든 경로를 지나 원래 지점을 돌아왔을 때, 최종적으로 음수가 되는 경우
- But, 음수 사이클은 존재해서는 안된다.
구현 방법
: A→B로 가는 경로보다 A→X→B로 가는 경로가 더 짧다면 갱신 !
- 초기 V^2 크기의 배열(dist) 내에 있는 모든 값을 INF로 채워준다.
- 주어진 그래프에서 간선에 적혀있는 숫자들을 dist 배열에 적어준다.
2-1) 자기 자신으로 가는 최단 거리(dist[i][i])는 0으로 설정해준다. - dp[i][j] > dp[i][k] + dp[k][j]를 만족하는 경우, dp[i][j]를 dp[i][k] + dp[k][j]로 갱신한다.
최종 구현 코드
import sys
INT_MAX = sys.maxsize
# 변수 선언
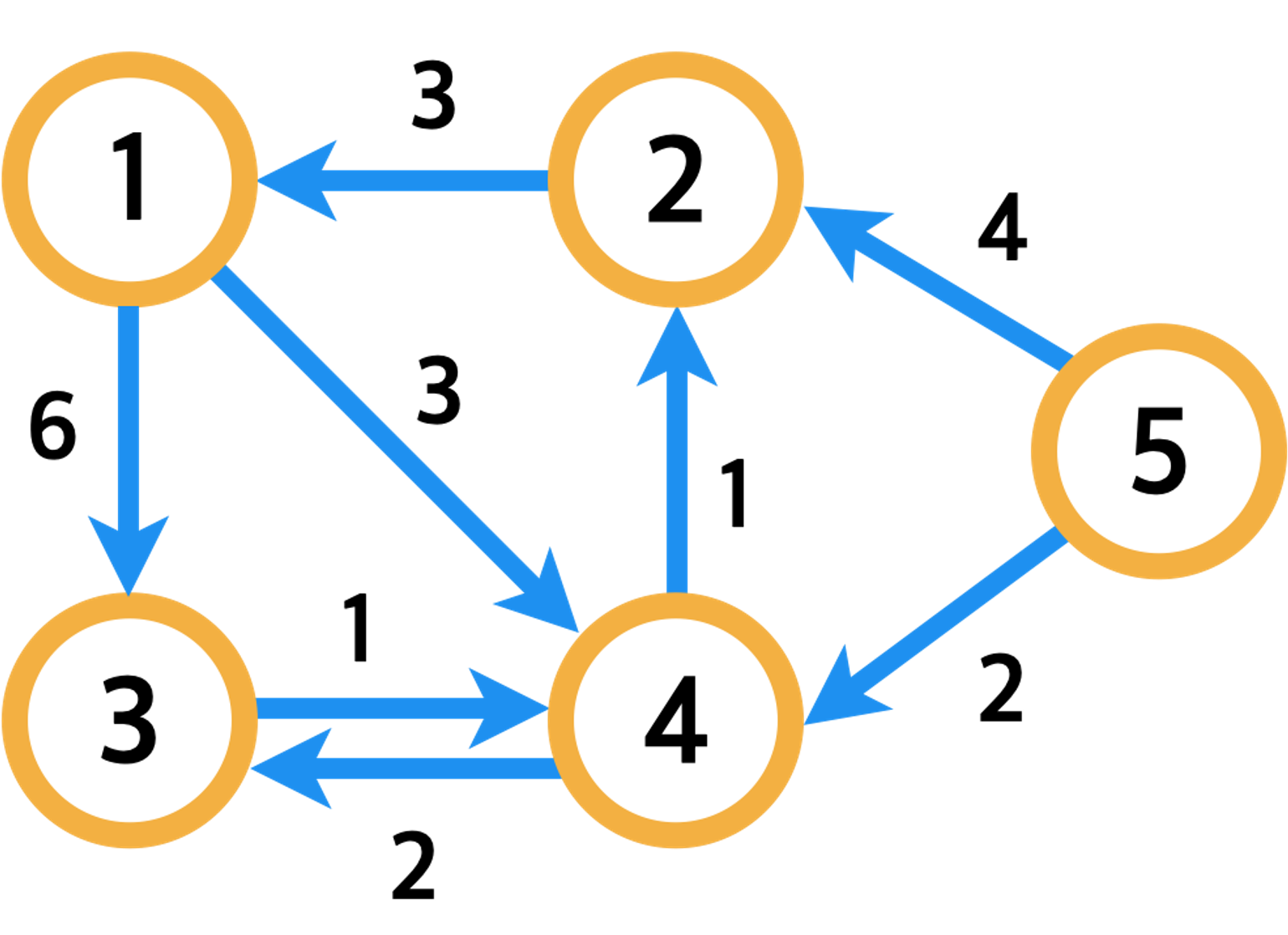
# 정점의 수 : 5, 간선의 수 : 8인 그래프
n, m = 5, 8
# dist 초기값을 전부 아주 큰 값으로 설정
dist = [
[INT_MAX] * (n + 1)
for _ in range(n + 1)
]
# 자기 자신으로 가는 값은 0으로 설정해줘야 함에 유의합니다.
for i in range(1, n + 1):
dist[i][i] = 0
# 주어진 간선 정보 (x, y, z)
# x -> y로 향하는 간선이 있으며, 가중치는 z
edges = [
(-1, -1, -1),
(2, 1, 3),
(1, 4, 3),
(4, 2, 1),
(5, 2, 4),
(5, 4, 2),
(4, 3, 2),
(3, 4, 1),
(1, 3, 6)
]
# 그래프를 인접행렬로 표현
for i in range(1, m + 1):
x, y, z = edges[i]
dist[x][y] = min(dist[x][y], z)
for k in range(1, n + 1): # 확실하게 거쳐갈 정점을 1번부터 N번까지 순서대로 정의합니다.
for i in range(1, n + 1): # 고정된 k에 대해 모든 쌍 (i, j)를 살펴봅니다.
for j in range(1, n + 1):
# i에서 j로 가는 거리가 k를 경유해 가는 것이 더 좋다면
# dist[i][j]값을 갱신해줍니다.
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
# 모든 쌍에 대한 최단거리 결과를 출력합니다.
for i in range(1, n + 1):
for j in range(1, n + 1):
# 불가능한 경우에는 -1을 출력합니다.
if dist[i][j] == INT_MAX:
print(-1, end=" ")
else:
print(dist[i][j], end=" ")
print()
REFERENCE
코드트리
'[Algorithm] 알고리즘' 카테고리의 다른 글
| 이진 탐색 (0) | 2024.07.09 |
|---|---|
| 그래프 (1) | 2024.07.09 |
| [Python][백준1931] 회의실 배정 (3) | 2024.07.02 |
| 그리디(Greedy) 알고리즘 (1) | 2024.07.02 |
| DFS와 BFS (2) | 2024.06.27 |
